Diving deep into TLSNotary

This document is an attempt to explain TLSNotary and its cryptographic underpinnings, DEAP. It also sheds light on the practical bottlenecks when using this system in production and outlines the future steps on the TLSNotary roadmap. A cooler and perhaps more appropriate title for the document could be "Diving Deep into DEAP," but "Diving Deep into TLSN" was chosen as it might resonate more broadly with the audience :)

TLS secures all connections on the internet today. In TLS, we have two parties: the client and the server. The first step in the TLS protocol is the TLS handshake, in which the client verifies the identity of the server by verifying their domain certificates and also generates a pair of symmetric keys that are used to encrypt further communication between the server and the client.

The use of symmetric keys for encryption prevents the client from forwarding the encrypted server response to a third-party verifier and convincing them about the authenticity of the response because the client also has the symmetric keys and thus can forge any arbitrary response allegedly coming from the server.

TLSNotary presents a solution to the above problem by splitting the session key between the Prover and the Verifier (Notary). With only a partial session key, the Prover is unable to forge server responses. In TLSN, the Verifier and the Prover run the 2PC-TLS protocol between them and together emulate the client in the TLS protocol. At the end of the 2PC-TLS protocol, the Verifier is convinced about the authenticity of the server response.

Simple 2PC-TLS protocol

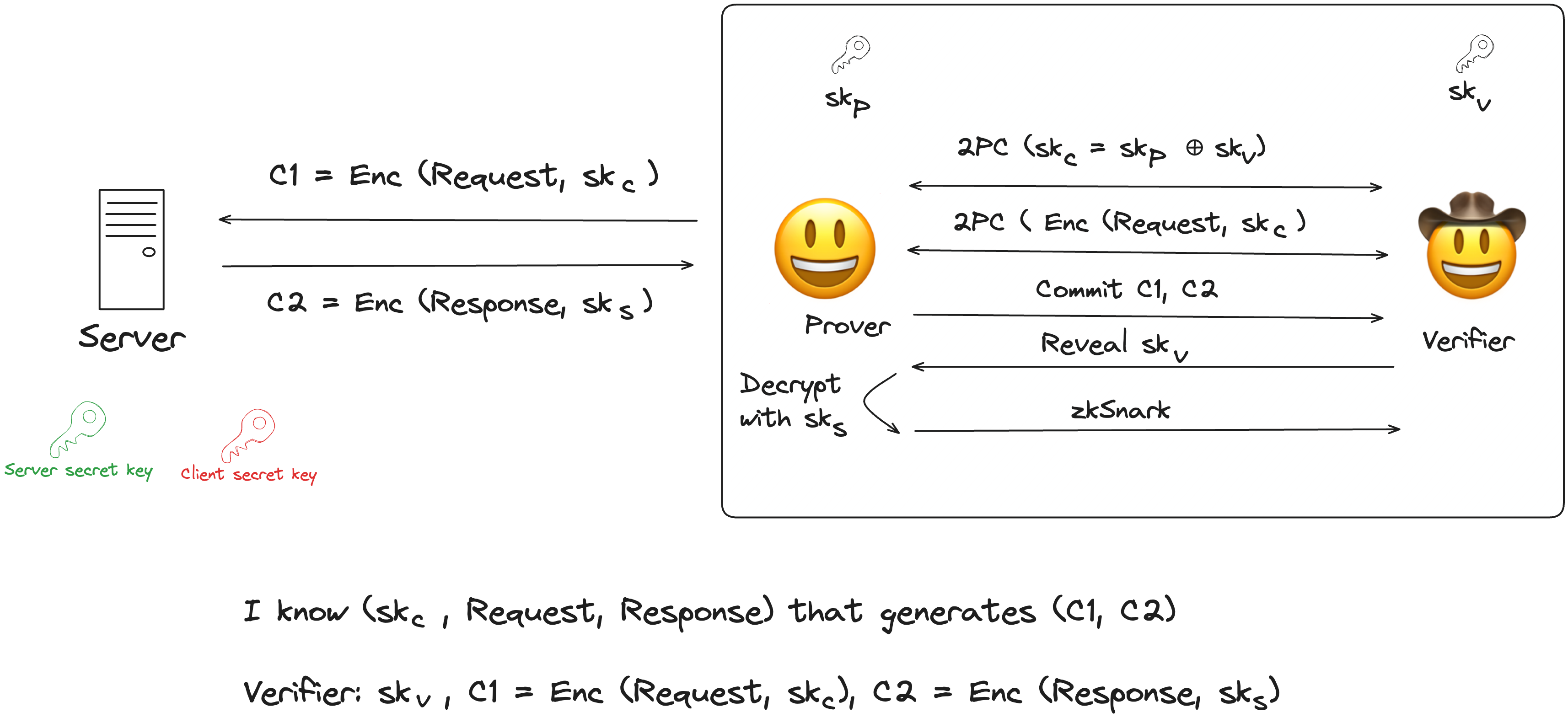
1. Perform the 2PC-TLS handshake with the server. At the end of the handshake, the server has it's complete session keys. The prover and the verifier have a share of the session keys, sk_p and sk_v respectively.
2. Perform 2PC-Encryption to compute the encrypted request C1 to the server.
   • Prover inputs: Plaintext p, sk_p
   • Verifier inputs: sk_v
   • Output: AES-GCM(p, sk_p ⊕ sk_v)
3. Send the encrypted request C1 to the server.
4. The server returns an encrypted response C2.
5. Forward the encrypted request C1, C2 to the Verifier.
6. The Verifier reveals their share of the secret key sk_v to the Prover.
7. The Prover generates a ZK proof that proves
   • They know (sk_c, p, r) such that
     • p encrypts to C1 under sk_c
     • r encrypts to C2 under sk_c
     • sk_c is formed from sk_p and sk_v
   • The prover also has the option to selectivel reveal parts of the plaintext request p and response r which the Verifier (Notary) attests to and makes the proof portable. Any third-party the trusts the Verifier (Notary) can verify the proof.

Malicious Garbler

The two-party computation in 2PC-TLS is performed using Garbled Circuits. zkPass has a great blog on Garbled circuits. Garbled circuits are secure against malicious evaluator but not secure against malicious garbler. If the function to be computed is f on Garbler's input x and Evaluator's input y, a malicious garbler can:

• Garble a different circuit f_g
• Feed a malicious input x_g
• Return malicious OT for the evaluator's input y_g

Privacy Leakage

Vanilla garbled circuits also suffer from the private input leakage attack vector. Essentially, the garbler could garble a different circuit f_g such that it leaks the evaluator's input y to them. Authenticated garbling schemes prevent these attack vectors but are costly in both compute and I/O.

DEAP

Simple DEAP

One solution for such attack vectors using the semi-honest garbled circuits is "Dual Execution". In these protocols, an honest original evaluator can garble the function f and let the original garbler, evaluate the circuit. To simplify, if Alice is Garbler and Bob is evaluator for the first execution, then Bob becomes the Garbler and Alice the Evaluator for the second execution. If the output of the first and the second execution match, then both the parties are satisfied about the correctness of the original evaluation and the output.

TLSN uses the Dual Execution With Assymetric Privacy (DEAP) scheme. In this scheme one of the parties has complete privacy while the other party reveals their private inputs during the protocol, hence the "assymetric" privacy. This construction works for TLSN because after the TLS session is closed, the security of the protocol is not compromised if the Notary shares their keys with the Prover.

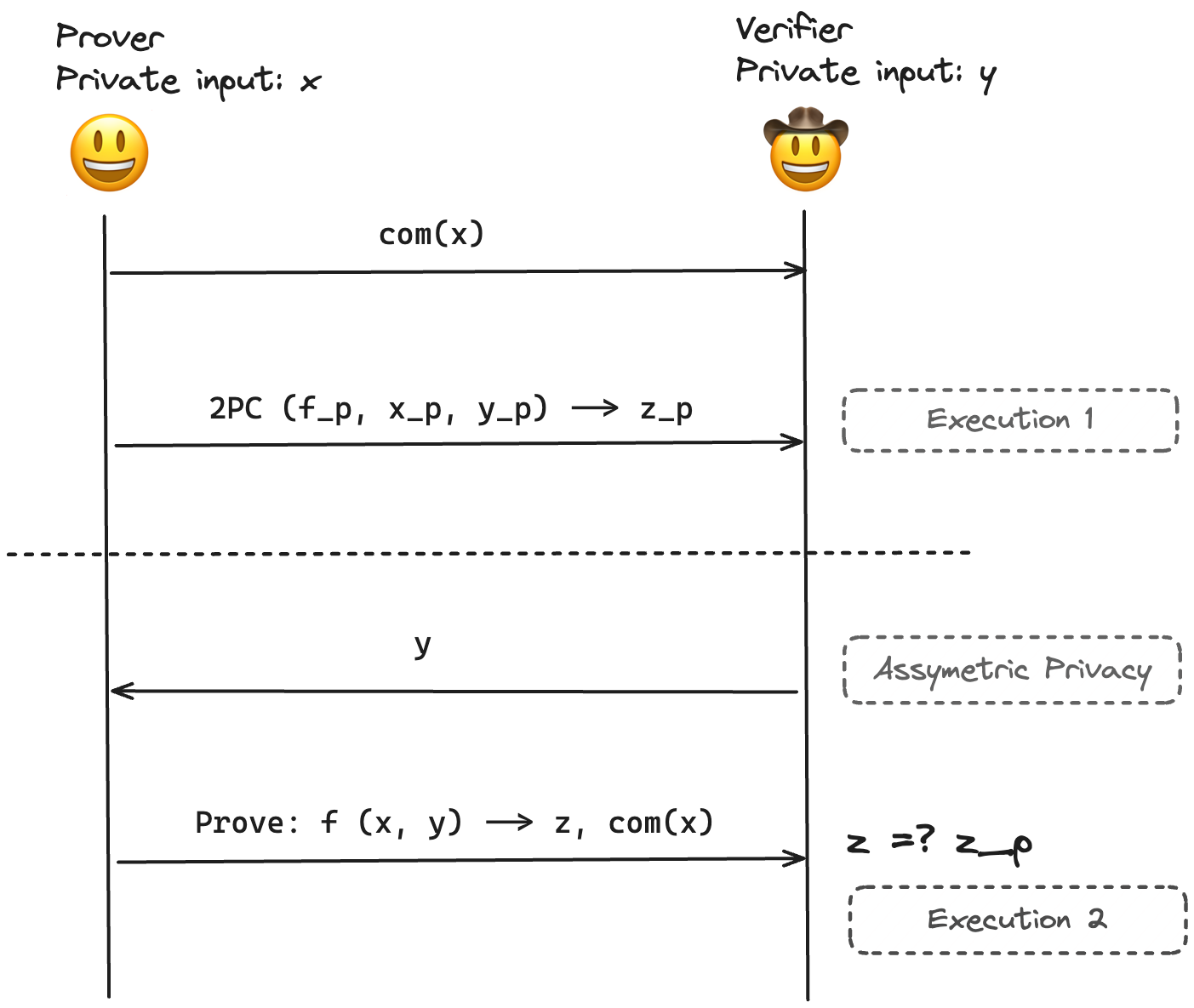
Above is a very simple diagram that explains DEAP. The function is executed twice thus "Dual exeuction". The verifier reveals their private inputs to the Prover after the initial phase, thus "Assymetric Privacy". The second exeuction proves:

• The correctness of function f executed in 2PC step
• Correctness of OT of verifier's input y in 2PC step
• Correctness of prover's inputs, i.e. existence of x that satisfies f(x, y) -> z. Note that this needs to be a ZK proof to preserve the privacy of x

The final check z =? z_p translates to f(x, y) =? f_p (x_p, y_p). f, y are public and known to the verifier. For a complex function f, a malicious Prover can satisfy the equation only if they are able to predict y, which is a random value generated by the Verifier.

Full DEAP

Notation

• x and y are Prover and Verifier's inputs, respectively.
• [x]_P and [y]_P are Prover and Verifier's encoded active inputs, respectively
• G denotes a garbled circuit for computing f(x,y)=z, where:
• Ev(G,[x],[y])=[z]
• d denotes output decoding information where De(d,[v])=v
• Δ denotes the global offset of a garbled circuit (I don't completely understand the revlevance of it)
• com denotes a commitment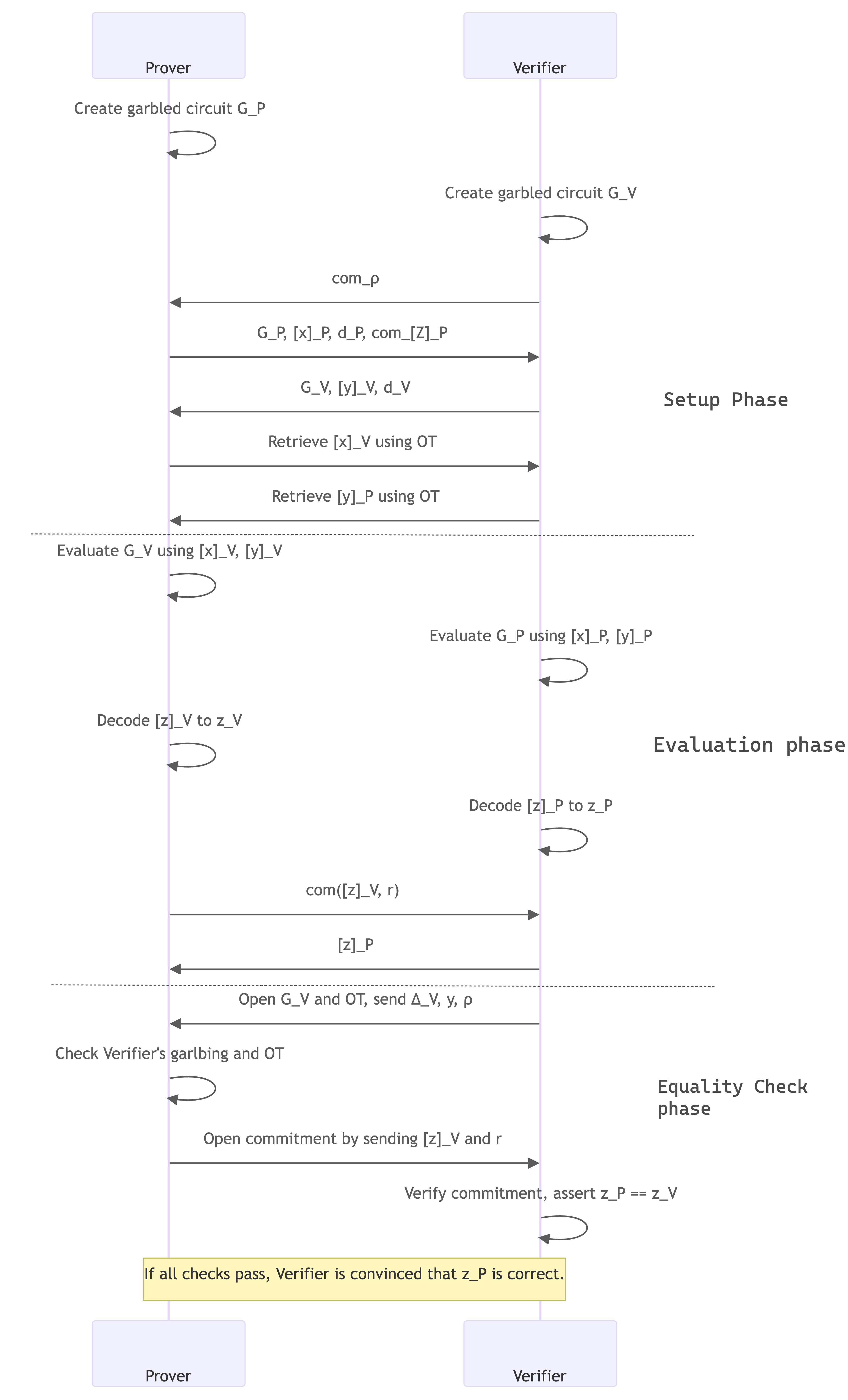

To reason about the above diagram, try replacing the 2PC step in simple DEAP with the detailed Garbled circuits step and the prove phase (second execution) with another Garbled circuits computation.

Important things to notice in DEAP

• Prover and Verifier both garble the same function f
• Prover uploads Garbled circuit G_P
• Prover downloads Garbled circuit G_V
• An honest Prover will get the correct output of f(x, y) immediately at the end of the evaluation phase. Thus they can choose to delay the equality check phase
• Prover evaluates the Verifier's Garbled circuit G_V and commits to the output [z]_V blinded using a random r, upon which the Verifier opens their garbling and reveals their key share. This allows the Prover to check that the garbling and OT were done correctly and that a potentially malicious verifier is not trying to extract the Prover's secret x. Once the Prover is convinced about the correctness of Verifier's garbling, it opens the commitment.
• Malicious Prover: If the Prover was malicious, the equality check will fail.

Note that DEAP uses garbled circuits to generate the ZK proof. Read their docs to understand the reasoning.

DEAP is one of the core building blocks of the 2PC-TLS protocol. Next we can dive deeper into the individual phases of the TLS protocol and see how DEAP is used in each phase.

Full 2PC-TLS protocol

Similar to the vanilla TLS version, 2PC-TLS can also be divided into three sub-parts: handshake, encryption and decryption.

2PC-TLS Handshake

This is still largely a black box for me. I have a very high level understanding of how 2PC-TLS handshake works. Hence skipped for now.

2PC-TLS Encryption

The 2PC-TLS encryption has two substeps:

1. Computing the encryption of the plaintext
   • This is achieved using DEAP
   • f is AES-CTR encryption function.
   • Prover's private inputs: p (Plaintext), Kp (Prover's private key)
   • Verifier's private inputs: Kv (Verifier's private key)
2. Computing the MAC of the cyphertext
   • I don't completely understand this phase yet. Hence skipped for now.

2PC-TLS Decryption

The 2PC-TLS Decryption has three substeps

1. Computing the MAC of the cyphertext
   • I don't completely understand this phase yet as well.
2. Computing the decryption of ciphertext
   • This is achieved using DEAP
   • Since, DEAP reveals the output to both parties, and we don't want to reveal the raw response with private data to the Verifier, we apply a mask on the ciphertext
   • f is Enc(Kp ⊕ Kv, ctr) ⊕ z
   • Prover's private inputs: Kp (Prover's private key), z (encryption mask)
   • Verifier's private inputs: Kv (Verifier's private key)
   • Prover removes the mask from the output ectr_z to get the plaintext, i.e. c ⊕ ectr_z ⊕ z = p, where ectr_z is output of 2PC computation and c is ciphertext returned from the server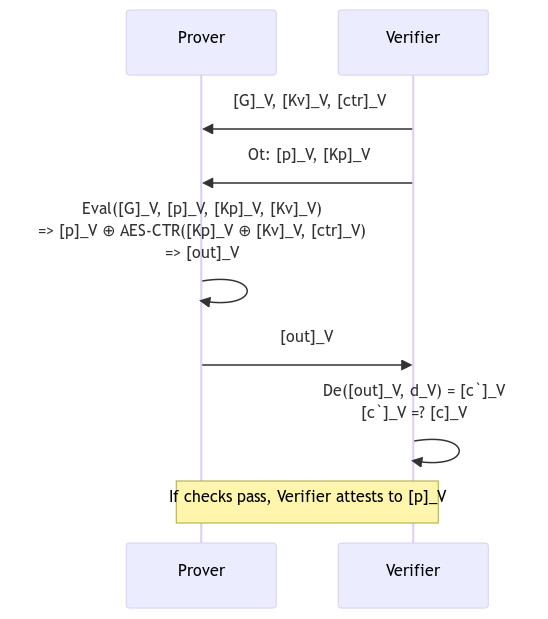
3. Proving the validity of plaintext
   • The prover needs to prove the validity of [p]N to the Verifier and it does using one round of vanilla GC

Implementation

Deferred Decryption

In the 2PC-TLS decryption step, once the Verifier has verified the MAC of the ciphertext response, the Verifier is convinced about the authenticity of the response. And if the Prover doesn't want to decrypt the response in 2PC, then the Verifier could just reveal their share of the key to the Prover using which the Prover can decrypt the ciphertext response. Thus effectively skipping step 2 in 2PC-TLS decryption above. This is fine, because we only care about the "authenticity" of the response which is guaranteed by the MAC check. Also, this helps save a lot of bandwidth. I'm yet to find a case where we might not need deferred decryption.

Deferred Equality Check (ZK in MPC-TLS)

The current implementation of TLSNotary defers the final equality check in DEAP for all the DEAP executions towards the end after the TLS session is closed. This is executed as the final step in MPC-TLS where all the equlity checks are done. Today, this "zk proof" is generated using Garbled circuits. As stated before, this equality check proves to the Verifier that all the garblings by the Prover were correct and there share of the secret key was not revealed prematurely.

Bottlenecks

Garbled circuits are bandwidth intensive. Since TLSN uses GC exetensively, TLSN is also a bandwidth-intensive protocol.

In MPC-TLS we perform AES-GCM using Garbled circuits in the following steps:

• 2PC-Encryption (Setup phase)
• 2PC-Encryption (Equality chck phase; ZK using GC)
• 2PC-Decryption (Setup phase; Skipped if deferred decryption)
• 2PC-Decryption (Equality check phase; ZK using GC; Skipped if deferred decryption)
• Proving validity of plaintext

1 AES Block (16 bytes) is 6500 AND gates.
In semi-honest 2PC that is DEAP, Half-gate GC costs 32 bytes/AND gate, so:

• => 6500 * 32 => ~208kB/block
• which means (208kB/block) / (16 bytes/block) = ~13kB/byte

Hence every byte in the plaintext contributes to 13kB of upload/download when encrypted/decrypted using GC. So, for a plaintext request oflp bytes and plaintext response of lr bytes

When Deferred decryption is NOT enabled:

• Net Prover upload:
  • [G]_p during encryption setup phase + [G]_p during decryption setup phase
  • lp * 13 + lr * 13 kB
  • (lp + lr) * 13 kB
• Net Prover download:
  • [G]_v during encryption equality check phase + [G]_v during decryption equality check phase + [G]_v during proving plaintext response
  • lp * 13 + lr * 13 + lr * 13 kB
  • (lp + 2 * lr) * 13 kB

When Deferred decryption is enabled:

• Net Prover upload:
  • [G]_p during encryption setup phase
  • lp * 13 kB
• Net Prover download:
  • [G]_v during encryption equality check phase + [G]_v during proving plaintext response
  • lp * 13 +lr * 13 kB
  • (lp + lr) * 13 kB

Note: We have not included the download/upload contributed due to 2PC-TLS handshake in the above calculations. I'm yet to understand 2PC-TLS in detail.

All these downloads and uploads can be preprocessed in the offline phase, i.e., done before the TLS connection is opened with the server. Once the TLS connection is opened with the server, the Prover and the Notary have around 10-30s before server timeout.

Future

Authdecode

This is a term that you will often see being thrown around for on-chain verification. It stands for "authenticated decoding". In the final step of 2PC-TLS decryption, the notary is convinced about the correctness of [p]_N. The Notary attest to [p]_N, but that means a third-party verifier verifying the attestation has to recompute the encodings and hash them. Because each byte is blown up to 8/128 bytes (not exactly sure), the hashing becomes too big to fit in a single block (or is too costly). The Authdecode protocol executed after the 2PC-TLS decryption, convinces the Verifier (Notary) about the correctness of the raw plaintext, which they can attest to. The plaintext length would be significantly smaller and can be hashed on-chain.

Quicksilver

Quicksilver will replace the use of Garbled circuits for ZK. It's a fast and cheap IZK protocol and would be run between the Prover and the Notary. This would mean we wouldn't have to use GC to prove the correct first execution and thus we would get rid of all downloads in the protocol. This is significant because even though download is comparitively "easier" than upload for Provers (users), download size is still signifcantly larger (lp + 2*lr)*13 (or (lp + lr) * 13) compared to upload (lp + lr)*13, as generally lr > lp, i.e. response is much bigger than the request.

After quicksilver with deferred decryption enabled:

• Net Prover upload:
  • [G]_p during encryption setup phase
  • lp * 13 kB
• Net Prover download:
  • [G]_v during encryption equality check phase + [G]_v during proving plaintext response
  • ~= 0 (Minimal amount of download because doen using Quicksilver)

Disclaimers

This explanation of DEAP and TLSNotary is pretty broad and might not nail all the details. It's meant to give you a starting point to understand TLSNotary and DEAP. To get a complete understanding, please refer to their docs and the respective papers.

• Quicksilver
• ZK using Garbled circuits (JKO13)